Empirical Bayes: UMBC Over Virginia

This year’s NCAA tournament finally brought the mother of all upsets: 16-seeded UMBC (the Retrievers!) beat the Virginia Cavaliers by 21 points!¹ Just how unlikely was UMBC’s upset?

To get a more precise without delving deeply into basketball metrics we can use Empirical Bayes as a framework for estimating the likelihood of a 16-over-1 upset. Our NCAA problem turns out to be especially suited for this approach because we’re asking a question about probabilities (this involves a Beta distribution) using win-loss data (“Bernoulli trials”). Under this setup, the probability of a 16-over-1 upset is described by a probability distribution $\mathrm{Beta}(\alpha, \beta)$. The function $\mathrm{Beta}$ gives us us the “probability of a probability”: it tells us what the probability of a 16-over-1 upset could be. Maybe it’s 1%, maybe 10%, etc.

We need two pieces of information to apply Empirical Bayes: an initial guess at the probability of an upset (a “prior” belief) and some hard data. The data is easy to gather; in the 33 years since the NCAA tournament format expanded to include 64 teams, 16 seeds had won zero games in $33 \cdot 4 = 132$ attempts.

Our “initial guess” is subjective, but it won’t turn out to matter much. For fun, let’s pick two extreme guesses and see how they affect our estimates.

• Prior 1: We have no idea what the probability of an upset is; it’s just as likely for a 16 to beat a 1 as for the reverse outcome. This is clearly not a realistic position, but it (in a sense) keeps us from imposing our point of view on the problem. This belief corresponds to a $\mathrm{Beta}(1,1)$ distribution.
• Prior 2: We’re pretty sure 1’s will beat 16’s; maybe call it 20-to-1 odds against an upset. This is a much stronger initial position and corresponds to an initial $\mathrm{Beta}(1, 20)$ distribution.²

Our two guesses look like this:

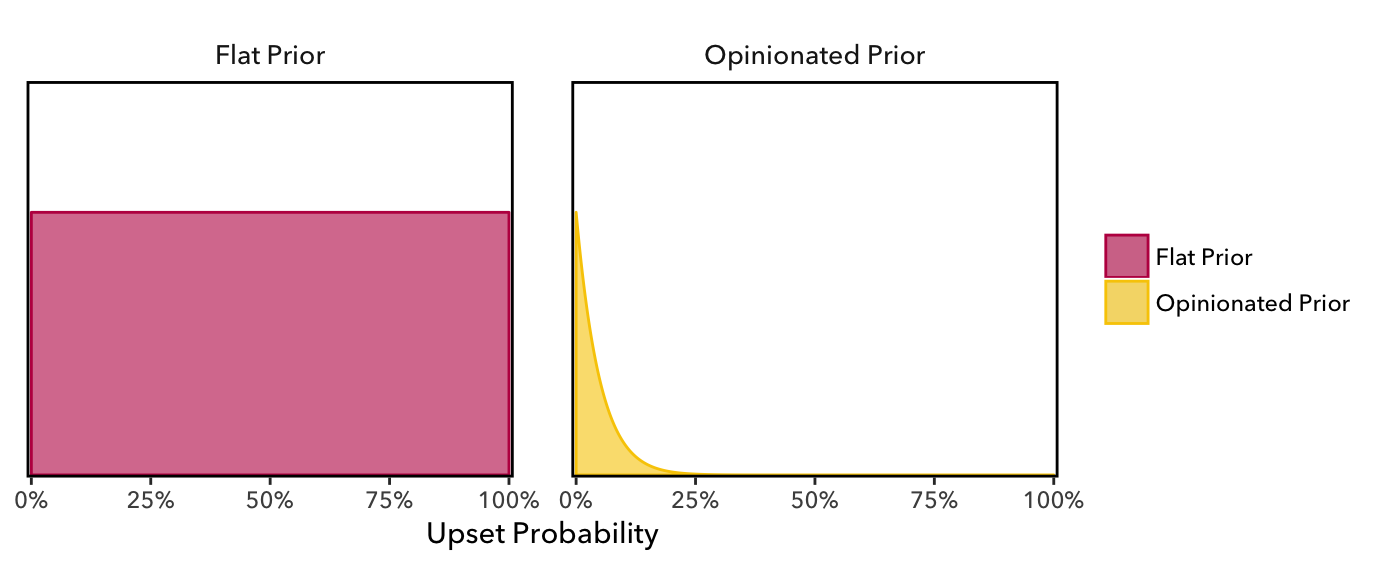
The first guess is completely flat; before seeing hard data, we do not claim to know if 16 seeds win 0% of the time, 55%, or 99%, etc. The second guess, though, is much more opinionated: we’re pretty sure that the 16 seed is going to lose.

Guess	99% CI Lower	99% CI Upper
Flat Prior	0	1.000
Opinionated Prior	0	0.197

With the “flat” prior, we don’t claim to know the probability of an upset: The 99% credible interval for the upset probability ranges from 0% to 100%. On the other hand, our 20-to-1 guess really does make an impact: The 99% CI ranges between 0% and 20%. That seems more reasonable.

Now, let’s add some data and answer the question: Going into this year, how unlikely was it that any individual 16 seed would beat a 1 seed?³ Since 1985 we’d observed 132 failures and zero successes, so we can update our initial guesses very easily: $\alpha_{2018} = \alpha_\mathrm{prior} + 0$ and $\beta_{2018}=\beta_\mathrm{prior} + 132$. This is possible because of the Beta distribution/Bernoulli trial problem type—they are conjugate priors:

• $\mathrm{Beta}(1, 1) \to \mathrm{Beta}(1, 133)$
• $\mathrm{Beta}(1, 20) \to \mathrm{Beta}(1, 152)$

The resulting probability distributions are below—we have to really zoom in to even see where the distribution is nonzero.

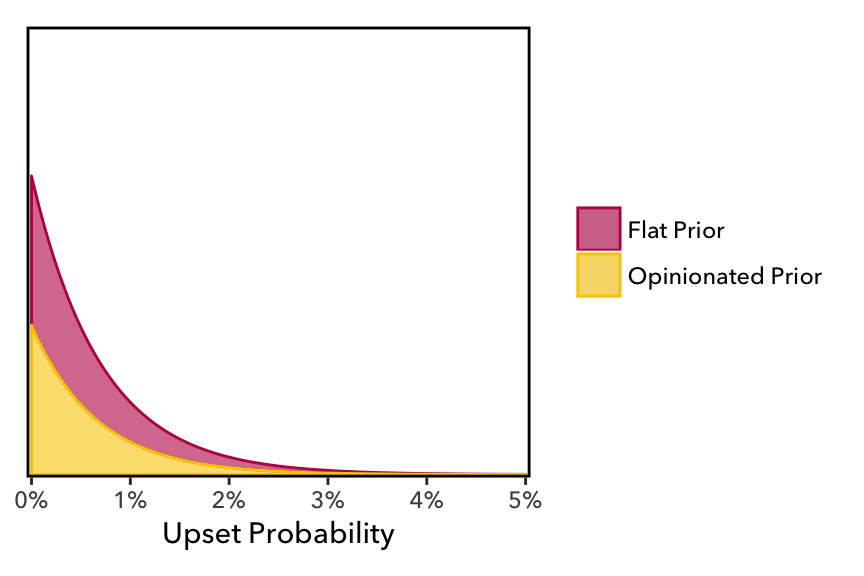
Two takeaways:

• These are very similar distributions.
• The probability of a 16-over-1 upset is very small (we are zoomed in 20 times on the $x$ axis).

Just how small is that probability?

Guess	Most Likely	99% CI Lower	99% CI Upper
Flat Prior	0	0	0.0340
Opinionated Prior	0	0	0.0298

Even for the flat prior, our 99% CI only ranges up to a 3.4% chance of upset. But, as promised, the opinionated prior hasn’t made much of a difference: incorporating our 20-to-1 guess only shrinks the probability to a 3% chance. In both cases, the most likely probability of an upset (the mode) is 0%!

So—we could not have ruled out an upset being impossible, given these results. That’s good, given what happened next! But, also happily, the estimated probability of an upset is very small and matches our intuition. Pretty cool!

Coda

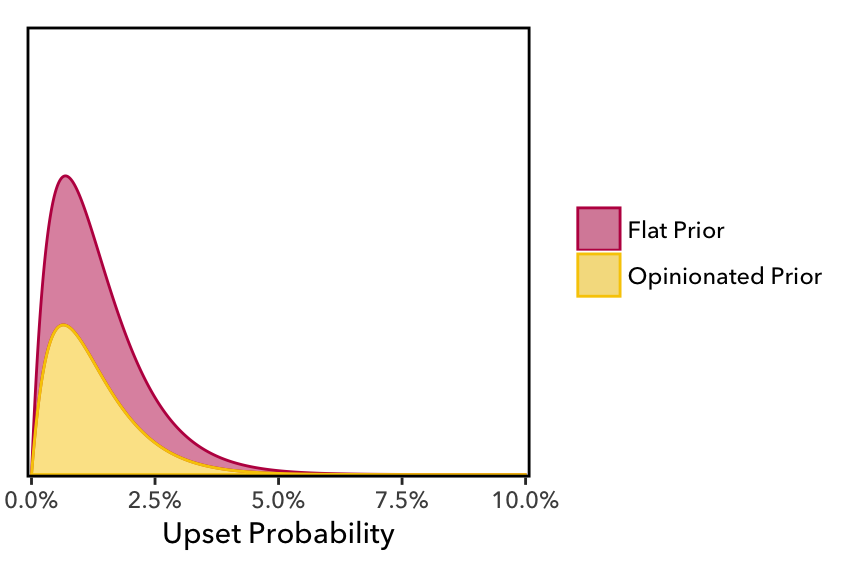
So…what about after this year? To find out, we just follow the same procedure as before, adding three non-upsets and our one shiny new upset. The posterior distributions are now:

• Flat Prior $\to \mathrm{Beta}(2, 136)$
• Opinionated Prior $\to \mathrm{Beta}(2, 155)$

And as a result, our updated probabilities are:

Guess	Most Likely	99% CI Lower	99% CI Upper
Flat Prior	0.0074	1e-04	0.0474
Opinionated Prior	0.0065	1e-04	0.0417

Still small, with the 99% CI ranging from about 0.01% to 4.7% and the most likely probability somewhere around 0.7%. But notice—now that we have finally observed an upset—that our posterior distribution no longer allows for a 0% chance of upset. As it shouldn’t!