Bayesian Coin Flips—The bcf Package

In an experiment with Approximate Bayesian Computation and R packages, I uploaded a new R package of my own to GitHub a few days ago named bcf for Bayesian Coin Flip. It simulates $N$-person games of skill, approximating these games as multiple players flipping coins with different “fairness parameters” $\theta_i \sim \mathrm{Beta}(\alpha_i, \beta_i)$. The first player to obtain a “Heads” result first wins, dealing with ties in a sensible way.¹

The ABC concept is well explained in a pair of articles. First, Rasmus Bååth introduces ABC through an exercise involving mismatched socks in the laundry (thanks for pointing me to this, Kenny). And Darren Wilkinson also does a nice job explaining how ABC works.

As far as bcf is concerned, the probability of a coin coming up Heads is picked from a distribution assigned to each player, $\theta_i^* \sim \mathrm{Beta}(\alpha_i, \beta_i)$. The package then simulates a set of games $d^*$ using these parameters and provides samples from the joint distribution $(d^*, \theta^*)$. Finally, by keeping only the data that match an observed result, we end up with a distribution proportional to the posterior $p(\theta|d)$.²

Example Usage

I built the package to better understand ABC and to humorously model our office’s dart-playing abilities. To keep things simple, the bcf package only provides a few functions: We can initialize a player, run a game, and use the results of the game to update a player’s statistics.

A basic game might go like so: We assume a pretty weak prior ($\theta \sim \mathrm{Beta}(1.2, 1.2)$) for each player before running a few games. After each game, we update the involved players.

In practice, I think it’s pretty easy to use. First, instantiate a few players:

library(bcf)

tom   <- new_player("Tom",   alpha = 1.2, beta = 1.2)
david <- new_player("David", alpha = 1.2, beta = 1.2)
kevin <- new_player("Kevin", alpha = 1.2, beta = 1.2)

print(tom)

## UUID:    d8cfe17e-c81d-11e7-9f88-f45c899c4b7b
## Name:    Tom
##
## Games:   0
## Wins:    0
## Losses:  0
##
## Est. Distribution:   Beta(1.200, 1.200)
## MAP Win Percentage:  50.000

Then simulate three games for which we already have results:

# Tom wins, David places second, Kevin finishes third
game_1 <- abc_coin_flip_game(
  players = list(tom, david, kevin),
  result = c(1, 2, 3),
  iters = 5000, cores = 5L)

## No. players:   3
## Assign result: 1, 2, 3
## Iters:         5000
## CPU cores:     5
## Workloads:     1000, 1000, 1000, 1000, 1000

tom   <- update_player(tom,   game_1)
david <- update_player(david, game_1)
kevin <- update_player(kevin, game_1)

# Tom wins, Kevin places second, David finishes third
game_2 <- abc_coin_flip_game(
  players = list(tom, david, kevin),
  result = c(1, 3, 2),
  iters = 5000, cores = 5L)


tom   <- update_player(tom,   game_2)
david <- update_player(david, game_2)
kevin <- update_player(kevin, game_2)

# Tom finishes second, David wins, Kevin finishes third
game_3 <- abc_coin_flip_game(
  players = list(tom, david, kevin),
  result = c(2, 1, 3),
  iters = 5000, cores = 5L)


tom   <- update_player(tom,   game_3)
david <- update_player(david, game_3)
kevin <- update_player(kevin, game_3)

bcf then provides methods for examining both players and games:

print(game_3)

## # A tibble: 6 x 6
##     Tom David Kevin outcome     n   pct
##   <dbl> <dbl> <dbl>   <chr> <int> <dbl>
## 1     1     2     3          1627  32.5
## 2     1     3     2          1917  38.3
## 3     2     1     3     ***   439   8.8
## 4     2     3     1           590  11.8
## 5     3     1     2           222   4.4
## 6     3     2     1           205   4.1

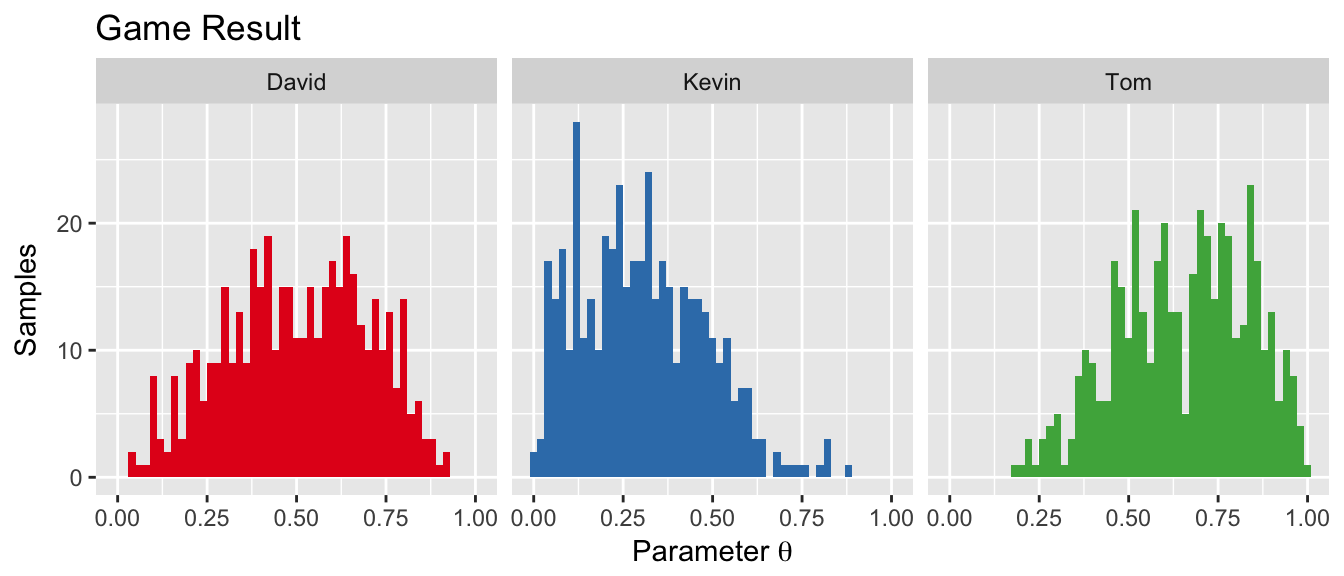
plot(game_3)

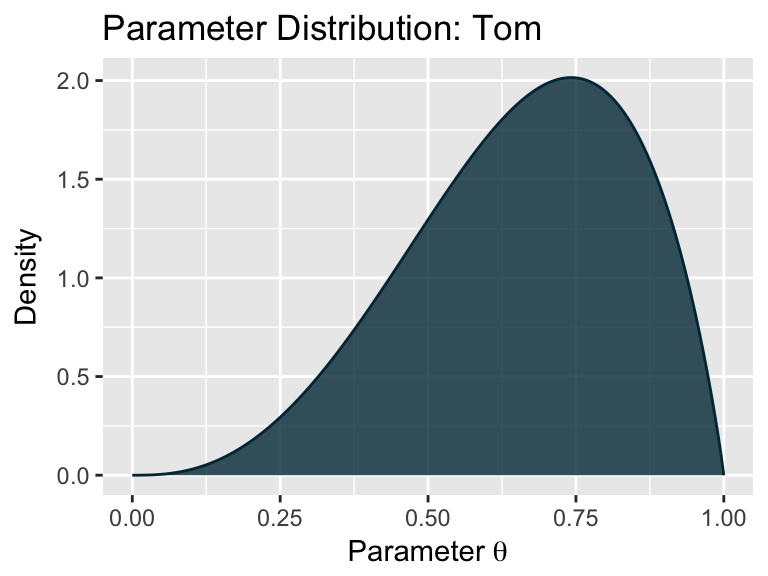
plot(tom)

This has been a pretty fun experiment in ABC and in R packaging. I’ll update this post if I ever return to the project.